Step 1 - Grayscale Conversion

Convert the image to grayscale. In MATLAB the intensity values of the pixels are 8 bit and range from 0 to 255.

Step 2 - Gaussian Blur

Perform a Gaussian blur on the image. The blur removes some of the noise before further processing the image. A sigma of 1.4 is used in this example and was determined through trial and error.

Step 3 - Determine the Intensity Gradients

The gradients can be determined by using a Sobel filter where $A$ is the image. An edge occurs when the color of an image changes, hence the intensity of the pixel changes as well.

Taking the derivatives will output:

Then, calculate the magnitude and angle of the directional gradients:

The magnitude of the image results in the following output:

Step 4 - Non Maximum Suppression

The image magnitude produced results in thick edges. Ideally, the final image should have thin edges. Thus, we must perform non maximum suppression to thin out the edges.

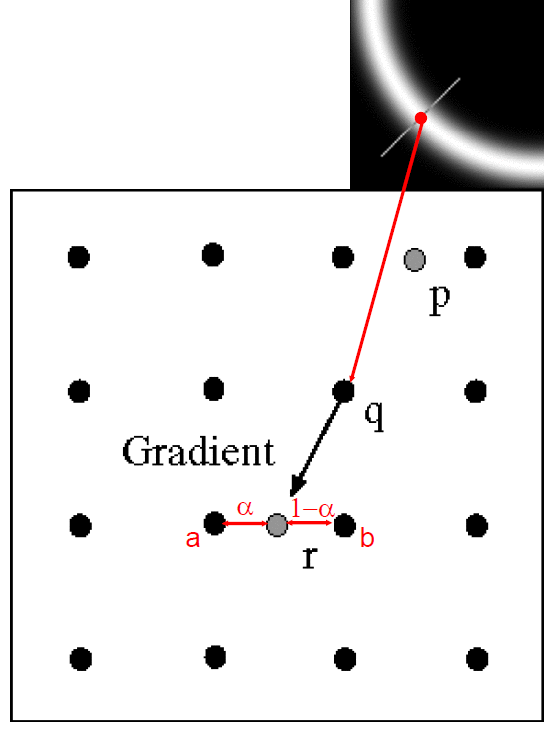
Non maximum suppression works by finding the pixel with the maximum value in an edge. In the above image, it occurs when pixel q has an intensity that is larger than both p and r where pixels p and r are the pixels in the gradient direction of q. If this condition is true, then we keep the pixel, otherwise we set the pixel to zero (make it a black pixel).

Non maximum suppression can be achieved by interpolating the pixels for greater accuracy:

The result of this is:

Non maximum suppression without interpolation requires us to divide the 3x3 grid of pixels into 8 sections. Ie. if the gradient direction falls in between the angle -22.5 and 22.5, then we use the pixels that fall between this angle (r and q) as the value to compare with pixel p, see image below.

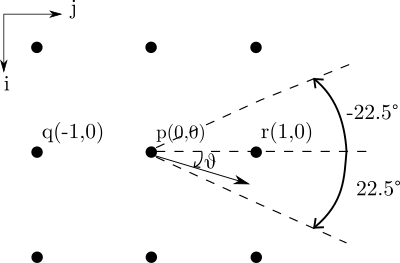
I found that using interpolation to give nicer results at the cost of a longer run time. Both implementations can be found on my github.

Step 5 - Double Thresholding

We notice that the result from non maximum suppression is not perfect, some edges may not actually be edges and there is some noise in the image. Double thresholding takes care of this. It sets two thresholds, a high and a low threshold. In my algorithm, I normalized all the values such that they will only range from 0 to 1. Pixels with a high value are most likely to be edges. For example, you might choose the high threshold to be 0.7, this means that all pixels with a value larger than 0.7 will be a strong edge. You might also choose a low threshold of 0.3, this means that all pixels less than it is not an edge and you would set it to 0. The values in between 0.3 and 0.7 would be weak edges, in other words, we do not know if these are actual edges or not edges at all. Step 6 will explain how we can determine which weak edge is an actual edge.

This threshold is different per image so I had to vary the values. In my implementation I found it helpful to choose a threshold ratio instead of a specific value and multiple that by the max pixel value in the image. As for the low threshold, I chose a low threshold ratio and multiplied it by the high threshold value:

highThreshold = max(max(im))*highThresholdRatio;
lowThreshold = highThreshold*lowThresholdRatio;

Doing this allowed me to successfully use approximately the same ratios for other images to successfully detect edges.

Step 6 - Edge Tracking by Hysteresis

Now that we have determined what the strong edges and weak edges are, we need to determine which weak edges are actual edges. To do this, we perform an edge tracking algorithm. Weak edges that are connected to strong edges will be actual/real edges. Weak edges that are not connected to strong edges will be removed. To speed up this process, my algorithm keeps track of the weak and strong edges that way I can recursively iterate through the strong edges and see if there are connected weak edges instead of having to iterate through every pixel in the image.

Step 7 - Cleaning Up

Finally, we will iterate through the remaining weak edges and set them to zero resulting in the final processed image:

Tadaa! Isn't that awesome?